|
理念、数学与“拯救现象”
--柏拉图的哲学、数学及其天文思想
 柏拉图(公元前427年—347年)是古希腊的大哲学家,苏格拉底(公元前469年—399年)的学生,亚里士多德(公元前384年—322年)的老师。 柏拉图(公元前427年—347年)是古希腊的大哲学家,苏格拉底(公元前469年—399年)的学生,亚里士多德(公元前384年—322年)的老师。
他一生大部分时间居住在古希腊民族文化中心的雅典。他热爱祖国,热爱哲学。他的最高理想:哲学家应为政治家,政治家应为哲学家。哲学家不是躲在象牙塔里的书呆,应该学以致用,求诸实践。有哲学头脑的人,要有政权,有政权的人,要有哲学头脑。公元前339年雅典民主派当权,苏格拉底被控传播异说,毒害青年,法庭判以死刑,苏格拉底从容答辩,竟以身殉。柏拉图目击心伤,终其身魂梦以之,不能忘怀。他从此不再打算参加政治活动,因为他觉得政治太丑恶肮脏了。
苏格拉底去世不久,柏拉图离开雅典,周游地中海地区,先后到了埃及,后来又来到意大利南部,访问毕达哥拉斯门徒所组成的学派。四十岁返回雅典,是年公元前387年。雅典西北角有一座以英雄阿卡德米(Akademia)命名的圣城,柏拉图家族在此附近有一座别墅,正当盛年的柏拉图下定决心,在此开设学园,招生讲学。学园的主要目的促进哲学的发展,准备了很多预备课程包括几何学、天文学、音乐学、算术等。当时有名学者登门造访,质疑问难,不仅成为雅典的最高学府,而且蔚为全希腊的学术中心。不少学生都是希腊城邦的世家子弟,世家子女!
柏拉图以继承苏格拉底大业为自任,放弃政治,讲学著书,孜孜不倦,苏格拉底一生不著一字,柏拉图以苏格拉底为主要对话者,先后共二十载,前后共著对话二十五篇,写成《理想国》。
《理想国》学问的综合性很强,书中讨论到优生学问题、节育问题、家庭解体问题、婚姻自由问题、独身问题、专政问题、独裁问题、共产问题、民主问题、宗教问题、道德问题、文艺问题、教育问题(包括托儿所、幼儿园、小学、中学、大学研究院以及工、农、航海、医学等职业教育)加上男女平权、男女参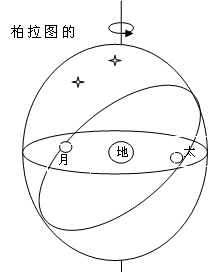 政、男女参军等等问题。古希腊人所谓知识,代表真理全部。柏拉图承先启后,学究天人,根深叶茂,山高水长。亚里士多德有句名言“吾爱吾师,吾尤爱真理”。 政、男女参军等等问题。古希腊人所谓知识,代表真理全部。柏拉图承先启后,学究天人,根深叶茂,山高水长。亚里士多德有句名言“吾爱吾师,吾尤爱真理”。
柏拉图的哲学中,有一种神圣高贵的特点,就是追求纯粹的理想。柏拉图认为真正实在的不是我们日常所见所闻的种种尝试和感觉,这些东西千变万化,转瞬即逝,是不牢靠的。真正的实在是理念,哲学的目的就是把握理念。理念具有超越的存在,它先于一切感性的经验,日常世界只是理念不完善的摹本。举例说,任何一张桌子都有这样那样的缺陷,不足以代表真实的桌子,只有桌子的理念才是完美无缺的。
在诸多的事物中,数学的对象更具有理念的色彩,虽然它也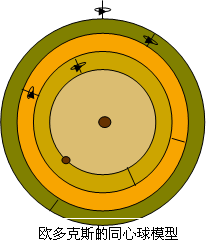 还不是理念本身。比如,我们所见到的任何一个圆都不是真正的圆,谁也不能说自己画得足够圆,我们所见到的任何一条线也不是真正的直线,因为真正的直线没有宽度,而且没有任何弯曲。真正的圆和真正的直线,不是我们感觉经验中的圆和直线,而就是圆的理念和直线的理念。他们是最容易领悟的理念,因此只有通过研究直线和圆这些几何对象更容易进入理念的世界。在柏拉图看来,数学是通向理念世界的准备工具,所以,柏拉图让人在学院门口立了一块牌子,上面写着:“不懂数学者不得入内。”表示他对数学十分重视。他的学园里数学研究得到了极大的发展,学得学生中出现了不少的大数学家。 还不是理念本身。比如,我们所见到的任何一个圆都不是真正的圆,谁也不能说自己画得足够圆,我们所见到的任何一条线也不是真正的直线,因为真正的直线没有宽度,而且没有任何弯曲。真正的圆和真正的直线,不是我们感觉经验中的圆和直线,而就是圆的理念和直线的理念。他们是最容易领悟的理念,因此只有通过研究直线和圆这些几何对象更容易进入理念的世界。在柏拉图看来,数学是通向理念世界的准备工具,所以,柏拉图让人在学院门口立了一块牌子,上面写着:“不懂数学者不得入内。”表示他对数学十分重视。他的学园里数学研究得到了极大的发展,学得学生中出现了不少的大数学家。
 柏拉图对数学的演绎方法的建立和完善起了重要的作用。他已经知道正多面体最多只有五种,即正四面体、立方体、正八面体,正十二面体、正二十面体。柏拉图的另一个最重要的发现:圆锥曲线。他利用直角、锐角和钝角圆锥,再用垂直于锥面一母线的平面来割每个锥面,这样依次得出了抛物线、椭圆以及双曲线的一支。 柏拉图对数学的演绎方法的建立和完善起了重要的作用。他已经知道正多面体最多只有五种,即正四面体、立方体、正八面体,正十二面体、正二十面体。柏拉图的另一个最重要的发现:圆锥曲线。他利用直角、锐角和钝角圆锥,再用垂直于锥面一母线的平面来割每个锥面,这样依次得出了抛物线、椭圆以及双曲线的一支。
柏拉图学生中数学最有成就的就是欧多克斯(公元前409—356年),他于公元前368年加入柏拉图的学园。他的主要数学成就是建立了比例论。越来越多的无理数的发现迫使希腊数学家不得不去研究这些特别的量,欧多克斯的贡献正在与引入了“变量”的概念,把数与量区分开来。在他看来,数(整数)是不连续的,而量不一定如此,比如那些无理数都可由量来代表。数与量的区分,方便了几何学的研究,为数学研究不可公度比提供了逻辑依据,人为地将数从几何学中赶了出去,使数学家不再关心线的长度,不再关心算术,而把精力全部投入几何学。
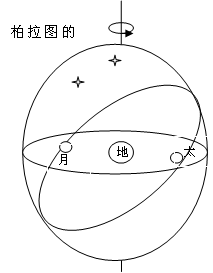
在天文学方面,柏拉图和毕达哥拉斯学派一样,深信天体是神圣高贵的,而匀速圆周运动又是一切运动之中最美最高贵的一种。所以,天体的运动应该是匀速的圆周运动。可是在天文观测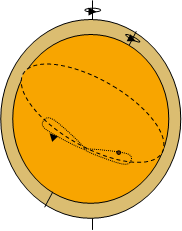 中,天上的有些星星的运转,有时向东,有时向西,时而快,时而慢,人们把这些星星叫做行星(希腊文中行星是漫游者的意思),但柏拉图对这种叫法不以为然,他相信就是行星也一定在遵循着某种规律性,也一定像恒星一样沿着绝对完美的路径运行。因此他给他的门徒们提出了一个任务:研究行星现在这个样子究竟是由哪些均匀圆周运动叠加而成的。这就是著名的“拯救现象”方法。“拯救”的意思就是行星的现象如此地无规则,如此的“不体面”,只有找出其所遵循的规则的高贵运动方式,才能洗刷这种“不体面”。这正如老子在《道德经》第四章中所说:“道冲,而用之或不盈。渊兮,似万物之宗;湛兮,似或存。吾不知谁之子,象帝之先。” 中,天上的有些星星的运转,有时向东,有时向西,时而快,时而慢,人们把这些星星叫做行星(希腊文中行星是漫游者的意思),但柏拉图对这种叫法不以为然,他相信就是行星也一定在遵循着某种规律性,也一定像恒星一样沿着绝对完美的路径运行。因此他给他的门徒们提出了一个任务:研究行星现在这个样子究竟是由哪些均匀圆周运动叠加而成的。这就是著名的“拯救现象”方法。“拯救”的意思就是行星的现象如此地无规则,如此的“不体面”,只有找出其所遵循的规则的高贵运动方式,才能洗刷这种“不体面”。这正如老子在《道德经》第四章中所说:“道冲,而用之或不盈。渊兮,似万物之宗;湛兮,似或存。吾不知谁之子,象帝之先。”
欧多克斯在毕达哥拉斯学派的宇宙途径基础上,用天球的组合来模拟天象,为柏拉图的理想提供了第一个有益的方案,即同心球的叠加方案。每个天体都有一个天球带动沿球的赤道运动,而这个天球的轴两端固定在第二个球上,第二个球又可以固定在第三个球上,这样组合出复杂的运动。欧多克斯发现,用三个球就可以复制出日月的运动,行星的运动则要用四个球,这样五大行星加上日月和恒星天,一个需要27个球。通过适当选取这些求得旋转轴、旋转速度和球半径,就可以使这套天球体系比较准确地再现所观测到的天体运动情况。这套希腊数理天文学的基本模式,基本上被后人完全继承了下来。
“拯救现象”方法是一种科学研究的纲领。我们面对的自然界,纷纭复杂,变化万千,如果不把它们纳入一个固定的框架之中,我们便不能很好地把握它们。拯救现象,正是将纷乱的现象归整。力图将天空中的漫游者固定起来或使其规则化,是与希腊当时的一个社会问题相对应的。当时雅典有许多流浪者,游手好闲,到处逛荡,让政府很头痛。希波战争期间,强行征募这些游民入伍,接受军队的规范和制约,较好地解决了这一社会问题。
老子在《道德经》第二十五章中说道:“有物混成,先天地生。寂兮寥兮,独立而不改,周行而不殆,可以为天地母。吾不知其名,强字之曰道,强为之名曰大。大曰逝,逝曰远,远曰反。故道大,天大,地大,人亦大。域中有四大,而人居其一焉。人法地,地法天,天法道,道法自然。”其哲学理念与柏拉图如出一辙。
柏拉图的学园培养了许多优秀的人物,亚里士多德就在这里当过学生,柏拉图在世的时候,他一直任学长。柏拉图学园遗址作为希腊文化的保存者存在了900多年,直到公元529年才被东罗马皇帝查士丁尼勒令关闭。
阿卡德米(Akademia)后来却成为了学院、研究院、学会(Academy)的代名词。再如:academia 学术生活和兴趣,学术环境; academic 学会的、研究院的,学究的书生气的,大学学生;大学教师,学究式人物;academical 大学礼服;academician 院士,学会会员;academicism 学院式,学院风气。
|
 网友评论:(只显示最新10条。评论内容只代表网友观点,与本站立场无关!)
网友评论:(只显示最新10条。评论内容只代表网友观点,与本站立场无关!)